DTPに必要な三角関数

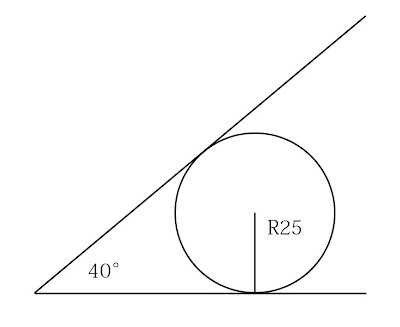
以下の図を作成するとき、どうしてますか？

人によってやり方は様々ですが、自分は今まで角度40を作成してから、半径25の円を眼見当で線分に接してました（恥

別なやり方として「三角関数」を使ってキッチリ作成する方法があります。

角度20で高さ25の直角三角形の幅を求めればいいわけです。

角度と高さから底辺と斜辺を計算サイトで求められます。

a=b/tan20 で、答えは68.68693548636。

印刷物にしてしまえば小数点第2位以下の誤差は分かりません。けれどデータを作成する上で眼見当で作成したのか、三角関数を使って作成したのかで、後で大きく違ってきます。

掲示板に神の啓示にある

Illustratorに貼り込まれた画像のサイズをリスト化する処理が必要となり、先週末からいろいろとトライしている。オブジェクトのプロパティからは幅と高さが参照できるのだが、どうやら回転がかかった場合は回転がかかった時の幅と高さになる模様。つまりオブジェクトの本来の幅と高さではなく、相対的な幅と高さということになる。対応策としては「回転を外した状態にしてから幅と高さを求める」というのが素直な考えだが、残念ながら回転の値が存在しない。IllustratorのオブジェクトはInDesignやQuarkXPressのようにボックスの左上を基準とした座標値や回転値などから場所を割り出すのではなく、6つのマトリックスを用いた方法で表現しているようで、ここらへんになってくるとお手上げだった。

上図で20°の角度が分からないから幅a'と高さb'が算出できないということ。

しかし角度が分かったとしても三角関数が理解できていないとa'とb'は出てこない。

35年前に高校を卒業してから一度も使ったことのない三角関数の復習をさせていただきました。

blogに書きながらの三角関数の復習です。

赤線の三角形は相似形なので角度は同じ。三角形の各辺の長さを求める公式は下図の場合

a=b/tanΘ もしくは a=c*cosΘ

b=a/tanΘ もしくは b=c*sinΘ

c=a/cosΘ もしくは c=b/sinΘ

これらの公式から

1.　79=a'*cos20+b'*sin20

2.　64=b'*cos20+a'*sin20

ここまででaとa'、bとb'とやったために分かりにくくなったな。。。と反省。

でもこのままいく。

要は上記の2つの式からb'を消せば、a'が導き出せる。

ここで中学で習った連立方程式がでてくる。

1. の両辺にcos20をかける　　2. の両辺にsin20をかける

1.　79*cos20=a'*cos20*cos20+b'*sin20*cos20

2.　64*sin20=b'*cos20*sin20+a'*sin20*cos20

1. の式から2. の式を引き算すればb'が消える。

79*cos20-64*sin20=a'*cos20*cos20-a'*sin20*sin20

整理すると

a'=(79*cos20-64*sin20)/(cos20*cos20-sin20*sin20)

同様のやり方で

b'=(79*sin20-64*cos20)/(sin20*sin20-cos20*cos20)

この辺は計算がやっかいなので

wolframalpha.com　がお薦め

よってa'=68.333、b'=43.236となる。基礎学力の大切さを改めて痛感した次第。。。